|
|
 |
Скорость. Сложение движений
|

Спортивную дистанцию 1,5 км хороший бегун пробегает примерно за 3 мин. 50 сек. (мировой рекорд 1958 г. – 3 мин. 36,8 сек.). Для сравнения с обычной скоростью пешехода – 1,5 м в секунду – надо сделать маленькое вычисление; тогда окажется, что спортсмен пробегает в секунду 7 м. Впрочем, скорости эти не вполне сравнимы: пешеход может ходить долго, целые часы, делая по 5 км в час, спортсмен же способен поддерживать значительную скорость своего бега только короткое время. Пехотная воинская часть перемещается бегом втрое медленнее рекордсмена; она делает 2 м в секунду, или 7 с лишком километров в час, но имеет перед спортсменом то преимущество, что может совершать гораздо большие переходы.
|
|
Подробнее...
|
|
Можно ли в 8 часов утра вылететь из Владивостока и в 8 часов утра того же дня прилететь в Москву? Вопрос этот вовсе не лишен смысла. Да, можно. Чтобы понять этот ответ, нужно только вспомнить, что разница между поясным временем Владивостока и Москвы составляет девять часов. И если самолет сможет пройти расстояние между Владивостоком и Москвой за это время, то он прибудет в Москву в час своего вылета из Владивостока.
|
|
Подробнее...
|
|
 Для нас, привыкших мерить время на свою человеческую мерку, тысячная доля секунды равнозначна нулю. Такие промежутки времени лишь недавно стали встречаться в нашей практике. Когда время определяли по высоте Солнца или длине тени, то не могло быть речи о точности даже до минуты; люди считали минуту слишком ничтожной величиной, чтобы стоило ее измерять. Древний человек жил такой неторопливой жизнью, что на его часах – солнечных, водяных, песочных – не было особых делений для минут. Только с начала XVIII века стала появляться на циферблате минутная стрелка. А с начала XIX века появилась и секундная стрелка.
Для нас, привыкших мерить время на свою человеческую мерку, тысячная доля секунды равнозначна нулю. Такие промежутки времени лишь недавно стали встречаться в нашей практике. Когда время определяли по высоте Солнца или длине тени, то не могло быть речи о точности даже до минуты; люди считали минуту слишком ничтожной величиной, чтобы стоило ее измерять. Древний человек жил такой неторопливой жизнью, что на его часах – солнечных, водяных, песочных – не было особых делений для минут. Только с начала XVIII века стала появляться на циферблате минутная стрелка. А с начала XIX века появилась и секундная стрелка.
|
|
Подробнее...
|
|
Когда Уэллс писал свой “Новейший ускоритель”, он едва ли думал, что нечто подобное когда-нибудь осуществится в действительности. Ему довелось, однако, дожить до этого: он мог собственными глазами увидеть – правда, только на экране – те картины, которые создало некогда его воображение. Так называемая “лупа времени” показывает нам на экране в замедленном темпе многие явления, протекающие обычно очень быстро.
|
|
Подробнее...
|
|
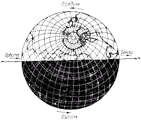
В парижских газетах появилось однажды объявление, обещавшее каждому за 25 сантимов указать способ путешествовать дешево и притом без малейшего утомления. Нашлись легковерные, которые прислали требуемые 25 сантимов. В ответ каждый из них получил по почте письмо следующего содержания:
“Оставайтесь, гражданин, спокойно в своей кровати и помните, что Земля наша вертится. На параллели Парижа – 49-й – вы пробегаете каждые сутки более 25 000 км. А если вы любите живописные виды, откиньте оконную занавеску и восхищайтесь картиной звездного неба”.
|
|
Подробнее...
|
|
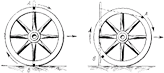 Прикрепите сбоку к ободу тележного колеса (или к шине велосипедного) цветную бумажку и наблюдайте за ней во время движения телеги (или велосипеда). Вы заметите странное явление: пока бумажка находится в нижней части катящегося колеса, она видна довольно отчетливо; в верхней же части она мелькает так быстро, что вы не успеваете ее разглядеть.
Прикрепите сбоку к ободу тележного колеса (или к шине велосипедного) цветную бумажку и наблюдайте за ней во время движения телеги (или велосипеда). Вы заметите странное явление: пока бумажка находится в нижней части катящегося колеса, она видна довольно отчетливо; в верхней же части она мелькает так быстро, что вы не успеваете ее разглядеть.
|
|
Подробнее...
|
|
Итак, не все точки движущегося колеса телеги перемещаются одинаково быстро. Какая же часть катящегося колеса движется всего медленнее?
|
|
Подробнее...
|
|
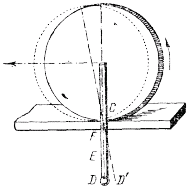 Вот еще одна не менее любопытная задача: в поезде, идущем, скажем, из Ленинграда в Москву, существуют ли точки, которые по отношению к полотну дороги движутся обратно – от Москвы к Ленинграду? Вот еще одна не менее любопытная задача: в поезде, идущем, скажем, из Ленинграда в Москву, существуют ли точки, которые по отношению к полотну дороги движутся обратно – от Москвы к Ленинграду?
Опыт с кружком и спичкой. Когда колесо откатывается налево, точки F, Е, D выступающей части спички подвигаются в обратную сторону.
|
|
Подробнее...
|
|
 Вообразите, что весельная лодка плывет по озеру, и пусть стрелка а на нашем рис. 11 изображает направление и скорость ее движения. Наперерез идет парусная лодка; стрелка b изображает ее направление и скорость. Если вас, читатель, спросят, откуда эта лодка отчалила, вы, конечно, сразу укажете пункт м на берегу. Но если с тем же вопросом обратиться к пассажирам весельной лодки, они указали бы совершенно другую точку. Почему? Вообразите, что весельная лодка плывет по озеру, и пусть стрелка а на нашем рис. 11 изображает направление и скорость ее движения. Наперерез идет парусная лодка; стрелка b изображает ее направление и скорость. Если вас, читатель, спросят, откуда эта лодка отчалила, вы, конечно, сразу укажете пункт м на берегу. Но если с тем же вопросом обратиться к пассажирам весельной лодки, они указали бы совершенно другую точку. Почему?
|
|
Подробнее...
|
|
|
|
|
|
|
|
|
|
 |